Nobel Prize in Physics 2023 for advances in attosecond science.

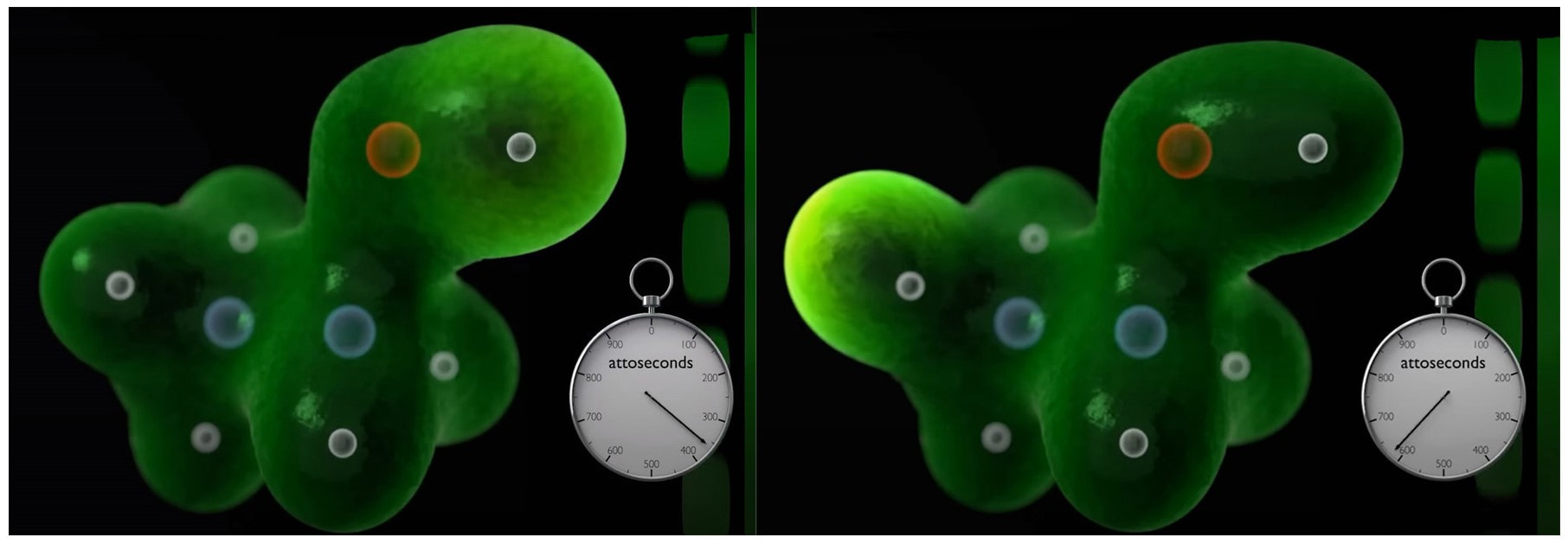
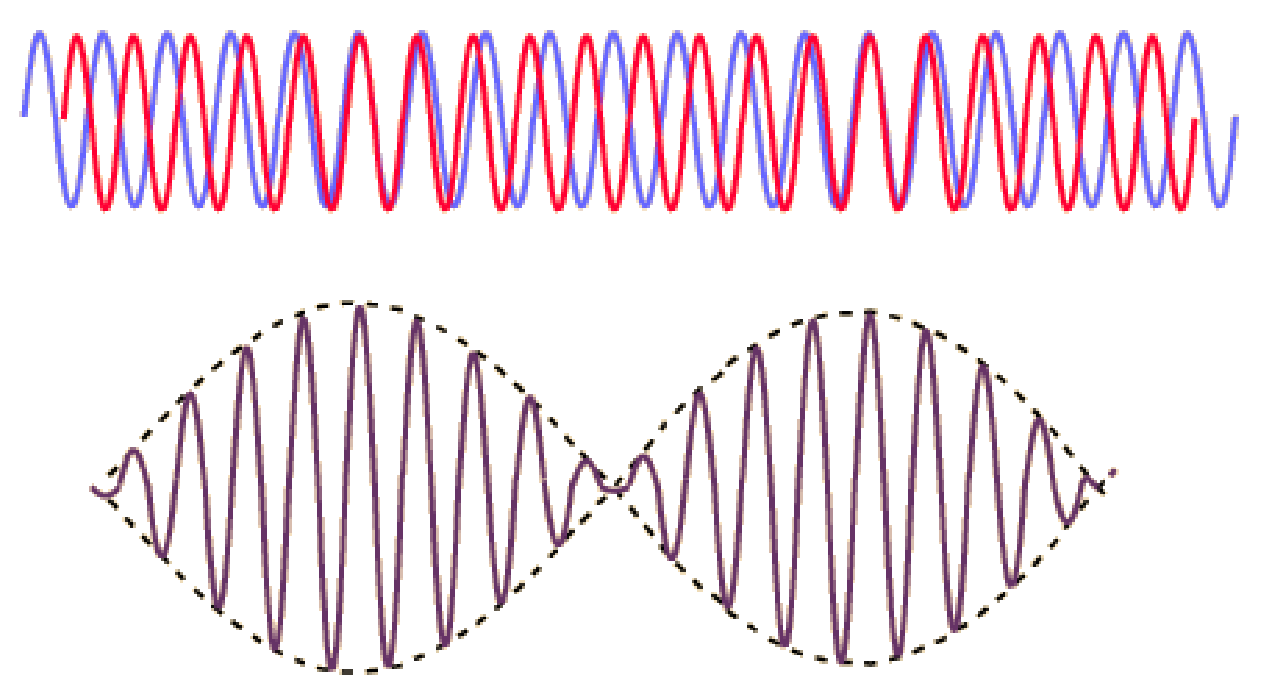
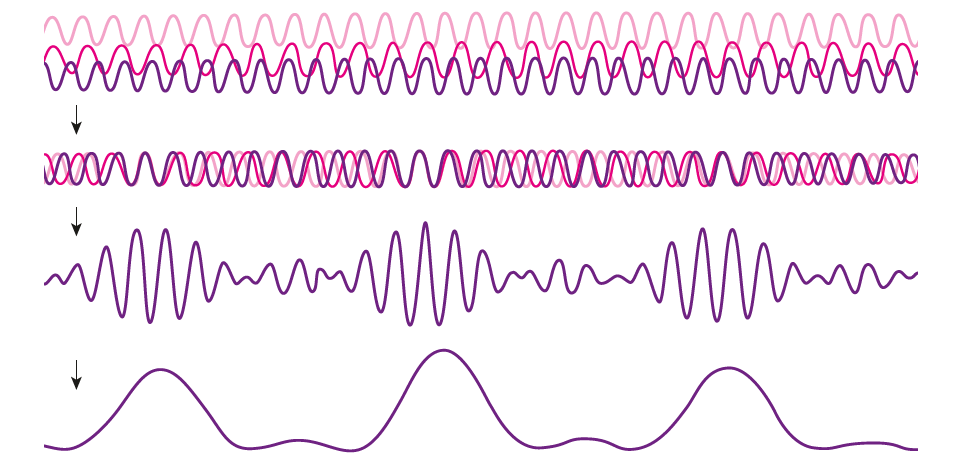
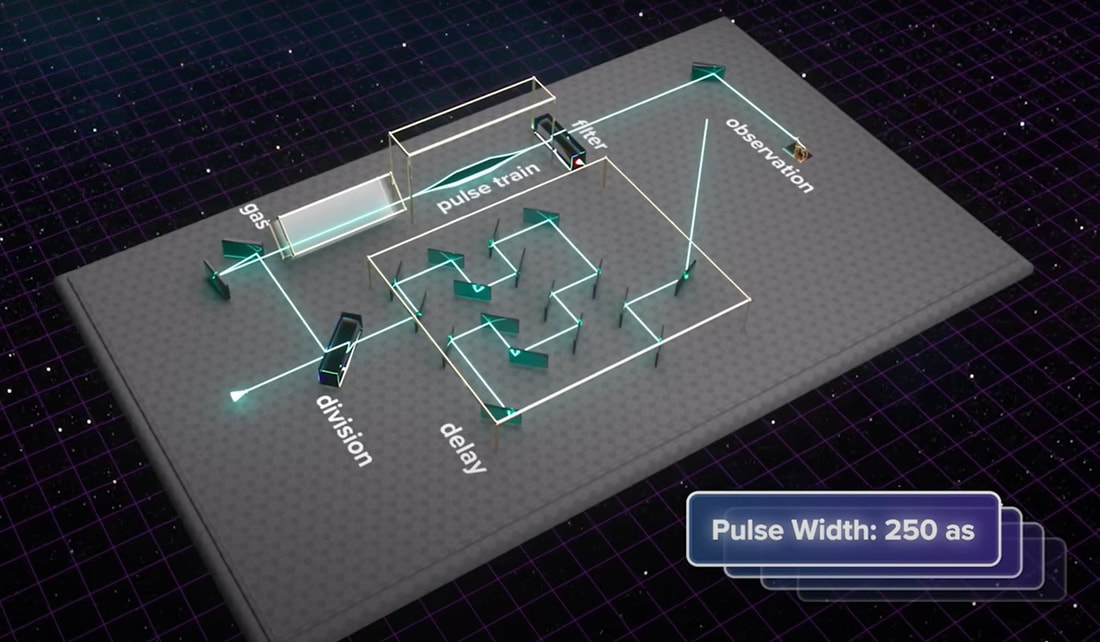
Graham writes …

Credit: News18.

The Nobel Prize in Physics 2023 has been awarded jointly to Anne L’Huillier of Lund University in Sweden, Pierre Agostini of Ohio State University in the USA and Ferenc Krausz of  the Ludwig Maximilian University in Munich, Germany, for their experimental work in generating attosecond pulses of light for the study, principally, of the dynamics of electrons in matter.

Nobel Laureates (L to R) Pierre Agostini, Anne L'Huillier and Ferenc Krausz. Credit: NEWS-DO.

​Effectively, the three university researchers have opened a new window on the Universe, and this will inevitably lead to new discoveries. Before we think about the applications of this newly-acquired technique, we need to explore the Nobel Laureates’ achievements in general terms.
 
Firstly it would be good to know, what is an attosecond (as)? It is a very short period of time, which can be expressed in variety of ways,
 
1 as      = a billion, billionths of a second,
            = 0.000 000 000 000 000 001 sec, or in ‘science-speak’,
            = 10^-18 sec.
 
Whichever way you think of it, it is an unimaginably short period of time. Other observers reporting on this have pointed out that there are more attoseconds in one second than there are seconds of time since the Big Bang! I don’t know if that helps? In general terms, what the research has led to is the development of a ‘movie camera’ with a frame rate of the order of 10 million billion frames per second. Effectively this allows the capture of ‘slow-motion imagery’ of some of the fastest known physical phenomena, such as the movement of electrons within atoms. If we think about objects in the macroscopic world, generally things happen on timescales related to size. For example, the orbits of planets around the Sun take years, and the time it takes for a human being to run a mile is measured in minutes and seconds. Another macroscopic object that moves very rapidly is a humming bird. Or rather, while it hovers statically to consume plant nectar its wings need to flap around 70 times per second, which is once every 0.014 sec. Clearly if we had a movie camera with a frame rate of, say 25 per second then the bird’s wings would simply be a blur. To examine each wing beat in detail, to study how the bird achieves its steady hover, then a minimum of maybe 10 frames per flap would be required. So, something like, at least, 1,000 frames per second would be advised to allow an informative slow-motion movie of the bird’s physical movements.

If we now consider the quantum world of particles and atoms, movements such as the dance of electrons in atoms are near-instantaneous. In 1925, Werner Heisenberg (one of the pioneers of quantum mechanics, and the discoverer of the now famous uncertainty principle) was of a view that the orbital motion of an electron is unobservable. In one sense he was correct. As a wave-particle, an electron does not orbit the atom in the same way as planets orbit the Sun. Rather physicists understand them as electron clouds, or probability waves, which quantify the probability of an electron being observed at a particular place and time. However, the odds of an electron being here or there change at the attosecond timescale, so in principle our attosecond ‘movie camera’ can directly probe electron behaviour. I’m sure that Heisenberg would have been delighted to learn that he had underestimated the ingenuity of 21st Century physicists. 

Electrons, or rather electron clouds, move around atoms and molecules with an attosecond timescale. Credit: PBS Space Time.

However, the ‘movie camera’ we have been discussing, is not a camera in the conventional sense. Instead a laser beam with attosecond period pulses is brought to bear on objects of interest (such as atoms within molecules, or electrons within atoms) to illuminate their frenzied movements. But how is this achieved?
 
L’Huillier team’s early work prepared the scene for attosecond physics. They discovered that a low frequency infra-red (heat radiation) laser beam passing through argon gas generated a set of additional high-energy “harmonics” – light waves whose frequencies are multiples of the input laser frequency. The idea of harmonics is a very familiar one in acoustics, and in particular those generated by musical instruments. The quality of sound that defines a particular instrument (its ‘timbre’) is determined by the combination of its fundamental frequency combined with its main harmonic frequencies. In music, the amplitude (or loudness) of the higher harmonics tends to decrease as the frequency increases, but one striking characteristic that L’Huillier found was that the amplitude of the higher harmonics in the laser light did not die down with rising frequency.

The next step was to try to understand this observed behaviour. L’Huillier’s team set about constructing a theoretical model of the process, which was published in 1994 (1). The basic idea is that the laser distorts the electric-field structure within the argon atom, which allows an electron to escape. This liberated electron then acquires energy in the laser field and when the electron is finally recaptured by the atom it gives away the acquired energy in the form of an emitted photon (particle of light). This released energy generates the higher frequency harmonic waveforms.
 
The next question was whether the light corresponding to the higher harmonic modes would interfere with each other to generate attosecond pulses? Interference is a commonly observed phenomenon, when two or more electromagnetic (or acoustic) wave forms are combined to generate a resultant wave in which the displacement is either reinforced or cancelled. This is illustrated in the diagram below. In this example, two wave trains with slightly differing frequencies are combined to produce the resultant waveform (this occurrence is called ‘beats’ in acoustics). Notice that the maximum outputs in the lower, combined wave train occur when the peaks in the original waves coincide, and similarly a minimum occurs when the peaks and troughs coincide to cancel each other out. 

A simple example of interference between two wave trains. The waves combine to either increase or cancel the wave amplitude to produce the lower wave form.

In the case of L’Huillier’s experiments, for interference to occur a kind of synchronisation between the emission of different atoms is required. If the atoms do not ‘collaborate’ with each other, then the output will be chaotic. In 1996 the team demonstrated theoretically that the atoms (remarkably) do indeed emit phased-matched light, allowing interference between the higher harmonics to occur, so opening the door to the prospect of attosecond physics. The image below illustrates the generation of attosecond pulses as a consequence of the interference between the various higher harmonic wave train outputs.

Top level shows a variety of higher harmonic waves, which are combined in the second level to give the resultant wave in level 3. This finally gives the sequence of pulses shown at the bottom of the figure.

​Over the subsequent years, physicists have exploited these detailed insights to generate attosecond pulses in the laboratory. In 2001, Agostini’s team produced a train of laser pulses, each around 250 as duration. In the same year, Krausz’s group used a different technique to generate single pulses, each of 650 as duration. Two years later, L’Huillier’s team pushed the envelope a little further to produce 170 as laser pulses.
 
So, the question arises, what can be done with this newly acquired ‘super-power’? Well in general it will allow physicists to study anything that changes over a period of 10s to 100s of attoseconds. 

As discussed above, the first application was to try something that the physics community had long considered impossible – to see precisely what electrons are up to. In 1905 Albert Einstein was instrumental in spurring the early development of quantum mechanics with his explanation of the photoelectric effect. The photoelectric effect is essentially the emission of electrons from a material surface, as a result of shining a light on it. He later won the 1921 Nobel Prize in Physics for this, and it is remarkable that he did not receive this accolade for the development of the theory of general relativity, which could be considered to be his crowning achievement. Einstein’s explanation showed that light behaved, not only as a wave, by also as a particle (the photon). The key to understanding was that the numbers of photo electrons that were emitted from the surface was independent of the intensity of the light and but rather depended upon its frequency. This emission was considered to take place instantaneously, but Krausz’s team examined the process using attosecond pulses and could accurately time how long it took to liberate a photoelectron.

Agostini's experimental set up. Credit: PBS Space Time.

The developments I have described briefly in this post suggest a whole new array of potential applications, from the determination of the molecular composition of a sample for the purposes of medical diagnosis, to the development of super-fast switching devices that could speed up computer operation by orders of magnitude – thanks to three physicists and their collaborators who explored tiny glimpses of time.
 
Graham Swinerd
 
Southampton, UK
December 2023
 
(1) Theory of high-harmonic generation by low-frequency laser fields, M. Lewenstein, Ph. Balcou, M. Yu. Ivanov, Anne L’Huillier, and P. B. Corkum, Phys. Rev. Vol. A 49, p. 2117, 1994.