New Physics? Part 2. A tale of wobbling Muons.

Graham writes …
 
Welcome back to this topic, which we discussed back in October’s blog post. As always in physics and biology, significant developments always happen, which have distracted me from writing further about the prospect of new physics.  It might be worth revisiting the October 2021 post to remind yourself briefly of some of the fundamentals that are relevant to today’s discussion.

As discussed then, one of the main theoretical pillars of the very small – the world of atoms and subatomic particles – is the standard model of particle physics. On the one hand, we know that the theory is ‘right’ in a very fundamental way, as we can perform detailed calculations to predict the results of experiments very accurately. This is evident from what we shall see later in this post. However, on the other hand, we also know that the standard model is not comprehensive. Again, as discussed in October, the theory of gravity (Einstein’s general theory of relativity) persistently ‘refuses’ to be unified with the standard model. Also, the mysterious ‘dark universe’ – dark matter and dark energy – which is believed to comprise about 95% of the matter/energy in the Universe is missing from the model.  So, we know there’s lots to be done, but we really are not sure how to go about it. All we can do is attempt to find experimental results which are not in complete accord with the theory, and then probe what such an anomaly might mean for the model. The reason why I’m blogging today is to talk about a ‘strange’ experimental result, which has been reported recently by a team of scientists working at Fermilab near Chicago, Illinois. Given that this can be referred to as the ‘anomalous magnetic dipole moment of the muon’, or the ‘muon g-2 experiment’, we need to unpack some of the terminology to hopefully reveal something of what’s going on. So, where to start? Firstly, I’d like to look at a property of fundamental particles called spin.

---

I think we are fairly familiar with the notion of spinning objects. If we spin up a macroscopic object, like a wheel, it acquires something called angular momentum, and the amount of angular momentum depends upon the mass of the object, how the mass is distributed and how fast it is rotating. It is the rotational equivalent of linear momentum. So, in the same way as we avoid standing in front of objects with large amounts of linear momentum, like a car travelling at speed, we also know intuitively not to tangle with an object with a significant amount of angular momentum, such as a large, rapidly rotating wheel. If we reached out and tried to grasp the wheel to slow it down, its significant rotational inertia will cause us grief.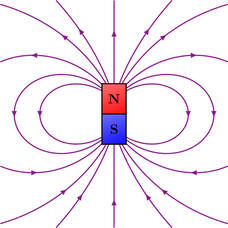 

Magnetic dipole field.

However, scientists also talk about spin when referring to sub-atomic particles such as an electron, for example. However, the properties of the ‘spin’ of an electron are very different to that of a macroscopic body. For one thing the angular momentum is quantised in terms of magnitude and direction. Also, such particles are considered to be infinitesimally small point particles, and as such talking about physical rotation makes no sense. But intriguingly they do possess intrinsic attributes that are usually associated with the property of rotation. Such particles also possess a magnetic field very similar to that produced by a tiny, simple bar magnet. This type of field is referred to as a magnetic dipole field, with the usual so-called north and south poles. You may have seen the structure of this field in a simple school experiment by sprinkling iron filings onto a piece of paper which has been placed on a bar magnet.  This type of magnetic field can be generated by the motion of an electric charge around a looped wire. So, we could imagine that electron is rotating, carrying its electric charge in a circular path around its axis of rotation, producing the magnetic field. However, we know that this cannot be so. If we were to envisage the electron as something other than a point particle, and try to use size estimates, its surface would have to be rotating faster than the speed of light to produce the measured dipole field strength!  It’s clear that particle spin is a difficult concept for everyone (not just me!) to appreciate intuitively. So, after all that, what is the dipole moment? Well, if we place the electron in an external magnetic field, the north-south axis of the particle’s field will align with the direction of the external field, as a compass needle rotates to align with the Earth’s magnetic field to indicate north. Hence the electron’s field exercises a torque, or moment, on the particles magnetic axis to bring this alignment, and this is referred to as the dipole moment. 

---

Another attribute of the particle which has its counterpart in macroscopic rotation is precession. If you think of a toy gyro and spin it up, then the force of gravity produces a torque which causes the axis of rotation to precess (or ‘wobble’), as illustrated in (the first half of) a video demonstration, which can be seen by clicking here. In a similar way, the magnetic axis of a particle (indicated by the the black arrow in the diagram) will also precess if placed in an external, uniform magnetic field (indicated by the green arrow). This is referred to as Larmor precession, after Joseph Larmor (1857-1942). 

---

I don’t know if you are still with me, but let’s come back to the media assertions about new physics, and the Fermilab announcement which mentions something called the ‘g-2 experiment’. The g here is referred to as the ‘g-factor’, which is a dimensionless quantity (a pure number) related to the strength of a particle’s dipole moment and its rate of Larmor precession. For an isolated electron, g = 2 according to Paul Dirac’s theory of relativistic quantum mechanics (QM), which he published in 1928. Subsequently, this theory has been superseded by the development of quantum electrodynamics (QED), which describes how light and matter interact. Using QED, we can perform the calculation for an electron that is not ‘isolated’. The g-factor calculation is not just about the interaction of the electron with the applied external magnetic field, but it is also influenced by interactions with other particles. This introduces another piece of quantum world terminology called quantum foam. This is the quantum fluctuation of the spacetime ‘vacuum’ on very small scales. Matter and antimatter particles are constantly popping into and out of existence so that the quantum vacuum is not a vacuum at all. For those of you with a bit of QM background, this is due to the time/energy version of the uncertainty principle. This idea was originally proposed by John Wheeler in 1955. Consequently, the electron also interacts with the quantum foam particles, and the influence of these short-lived particles affect the value of the g-factor, by causing the particle’s precession to speed up or slow down very slightly. The experimental value of the electron g factor has been determined as
 
g = 2.002 319 304 362 56(35)
 
where the part in brackets is the error.  The theoretical value of g-2 matches the experimental value to 10 significant figures, making it the most accurate prediction in all of science.

The muon is 207 times more massive than the electron.

So, we find that the behaviour of an electron conforms with theory very well, but what about other particles? The recent Fermilab experiment refers to similar work looking at a particle called a muon. So, what is this? The muon is a particle which has the same properties as an electron, in terms of charge and spin, but is 207 time more massive (see the blog post for October again, for details). It is also unstable, with a typical lifetime of about 2 microseconds (2 millionth of a second), but this is still long enough for the scientists to work with them. What the Fermilab team did was measure the muon’s g-factor in the same way that we have described for the electron. This time a difference between experiment and theory was observed,
 
g(theory) = 2.002 331 83620(86),
 
g(experiment) = 2.002 331 84121(82).
 
Of course, the difference is tiny, so why the big deal? Well, the theoretical value describing how the quantum foam influences the value has been determined using our current model of the subatomic world – that is, the particles and forces as described by the standard model of particle physics. The fact that the experimental value differs suggests that there may be new particles and/or forces that are currently absent from our understanding of the quantum world. Another question posed by this result is why does the electron conform and the muon not? In the theory, the degree to which particles are influenced by the quantum foam is proportional to the square of their mass. Since the muon is about 200 times heavier than the electron, it is approximately 40,000 times more sensitive to the effects of these spacetime fluctuations.

---

At the end of the day, do the Fermilab results have the status of a confirmed, water-tight discovery? Well, actually no. The degree of certainty at present is at the 4.2 sigma level, which suggests that there is a roughly one chance in 100,000 that the result could be a result of random chance. To get the champagne glasses out, and to start handing out Nobel prizes, further work is required to achieve a 5 sigma result (again see October’s post).
 
So, where does all this take us? The bottom line is that it tells us there are things about the quantum world that we don’t know – which, you could say, we knew already! But this is how physics works. To paraphrase Matt O’Dowd, Australian astrophysicist, “ … to find the way forward, we need to find loose threads in the [current] theories that might lead to deeper layers of physics. The g-2 experiment is just one loose thread that was begging to be tugged. The scientists at Fermilab have just tugged it hard …”. I await further developments!

Graham Swinerd

Southampton
March 2022

---